3.4.10 Complete the Square

Complete the Square applied to a quadratic expression .[a]⋅x^2+.[b]⋅x+.[c] rewrites the expression as

The expression can then be simplified, rooted, isolated and resolved.

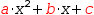
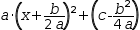
The mathematical rationale can be seen by performing the transformation step by step. Performing these steps is a good exercise in learning Myron.

It is easy to find roots for quadratics of the form (x-a)^2=b where a and b are constants because you can take the square root of both sides. For example, (x-4)^2=9 can be solved by modifying the equation (see §3.5.3) with the pattern √? to √((x-4)^2)=√9 and simplifying to x-4=3. Isolating x gives x=7.

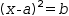
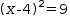
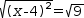
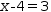
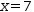
It is less easy to find the roots of an equation like x^2-8⋅x+7=0, which as it happens is the same as the equation in the previous paragraph. However, observe that x^2+b⋅x+(b÷2)^2=(x+b/2)^2, which can easily be proven by distributing the right side and simplifying. As a result, x^2-8⋅x=-7 can be rewritten x^2-8⋅x+(8/2)^2=-7+8/2^2. Using the observation, the left side is a perfect square. The equation can be rewritten (x-4)^2=9

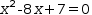
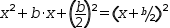
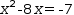
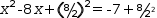
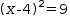
To deal with equations in which the coefficient of x^2 is not 1, modify the equation by dividing both sides by the coefficient.

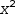
This leads to a scheme with the following steps to find the roots of a quadratic with the form a⋅x^2+b⋅x+c=0.

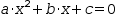
1. move c to the right side
2. divide both sides by a
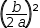
3. add (b÷(2⋅a))^2 to both sides
4. replace the left side with its perfect square
5. take the square root of both sides
6. isolate x and deal with the square root on the right side by symbolic simplification